The shape of a region

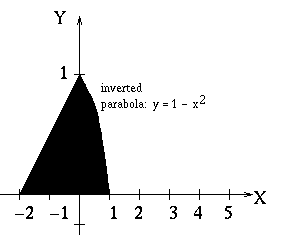
Look at the region below. Would you choose to integrate first in x and then in y (left to right, then bottom to top) or first in y then in x (bottom to top, then left to right)?

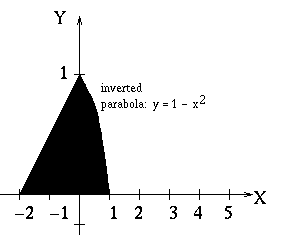
Let's see what happens if we choose to integrate bottom to top then left to right. Notice that the upper boundary is not one smooth function. This will cause some difficulties. In fact, the upper boundary is

$$y = \left\{ \begin{array} {ll} x/2 + 1, & -2 \le x \le 0 \\ 1 - x^2 & 0 \le x \le 1 \end{array} \right.$$

Thus, for this choice of the order of integration, we have the boundaries:

left x = -2

right x = 1

bottom y = 0

$$y = \left\{ \begin{array} {ll} x/2 + 1, & -2 \le x \le 0 \\ 1 - x^2, & 0 \le x \le 1 \end{array} \right.$$ top

This will lead us to a rather complicated iterated integral.

If we choose the other order of integration (which is the better choice,) we see that the left and right boundaries are both smooth functions. We can determine these functions by rearranging the equations given so that we have x as a function of y. This produces:

left x = 2(y - 1)

$$x = \sqrt{1 - y}$$ right

bottom y = 0

top y = 1

Note that the bottom and top boundaries are the minimum value and maximum value of y that occur over the region. We are left with setting up the integral as

$$\int_R fdA = \int_0^1 \left( \int_{2(y-1)}^{\sqrt{1-y}} f(x,y) dx \right) dy.$$

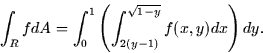
If we choose the original order of integration, we have to break R into two regions:

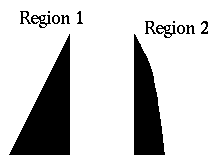
which results in the integral

$$\int_R fdA = \int_{-2}^0 \int_0^{\frac{1}{2} x + 1} f(x,y) dy dx + \int_0^1 \int_0^{1 - x^2} f(x,y) dy dx.$$

In general, we want to integrate bottom to top first if the bottom and top boundaries are described by smooth functions of x. If the left and right boundaries can be described by smooth functions of y then integrate left to right first. If they're all smooth, it's your choice, unless the function prefers an order. If none are smooth, choose the order that result in breaking the Region up into the smallest number of integrals.