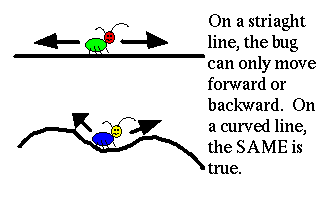
Think of a curve in space. How many variables do you need to describe that curve completely? The answer is one. No matter how many dimensions the space is, the curve still only needs one variable to describe it. Think about it this way. If you stretched a piece of string out tightly and a bug started to walk from left to right, how many quantities would it need to specify its location? It would suffice to describe its position as a distance from the starting point. This only requires a single number, the total distance the bug has traveled.

What if the string is now twisted and bent into a strangely shaped path? Nothing really changes. The bug can still specify its position as the distance from the point where it started walking.
Thus, a curve (in this case the string) is a one-dimensional object since it can be described by only one parameter or variable. We say that the one-dimensional curve is embedded in a space of higher dimension. This means that from the bug's perspective, the curve is one dimensional. From the perspective a being outside the curve, the space looks twisty, but it is still a one dimensional object. For a really entertaining look at the different perspectives you can have from spaces of different dimension, try reading Flatland by E. Abbott.