Since a curve is one dimensional, we only need a single parameter to describe it. Usually this parameter is denoted t and sometimes has the additional meaning of representing time in more physical applications. To fully specify how the curve moves in three-dimensional space we will need to give x, y, and z as functions of t. We also need a range of values for t. A parameterization of a curve is the specification of these quantities:
| (1) |
It is also important to make sure that the range of values for t is such that the curve is only traced out by the parameterization once.
When we say that a parameterization traces out a curve, we mean that
if we specify a point on the curve as (x(t),y(t),z(t)) and vary t, the
collection of points specified in this manner make up the curve. Another
way, that is more common, is to use the notation of the position vector.
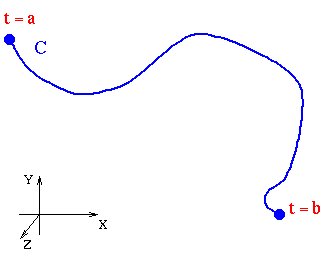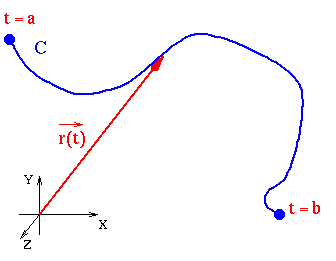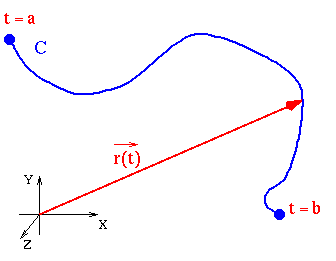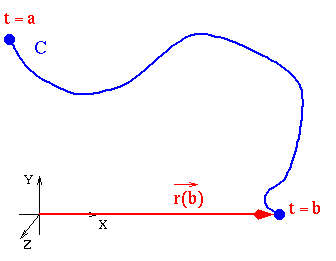
We let the vector ![]() .The tail of this vector sits at the origin, and the tip of this vector is
at a pint on the curve. As t varies over its possible values, the tip
traces out the curve. When we draw a curve from a parameterization, we
usually put an arrow along the curve in order to indicate the direction of
increasing t.
.The tail of this vector sits at the origin, and the tip of this vector is
at a pint on the curve. As t varies over its possible values, the tip
traces out the curve. When we draw a curve from a parameterization, we
usually put an arrow along the curve in order to indicate the direction of
increasing t.