Suppose that ![]() is the position of a particle over some time
interval. The instantaneous velocity of the object tells us two things.
First, it tells us how fast the object is moving (its speed). Second, it
tells us in what direction it is moving. Since the velocity has a
direction and a magnitude, it must be a vector. Thus, in three dimensions,
the velocity, denoted
is the position of a particle over some time
interval. The instantaneous velocity of the object tells us two things.
First, it tells us how fast the object is moving (its speed). Second, it
tells us in what direction it is moving. Since the velocity has a
direction and a magnitude, it must be a vector. Thus, in three dimensions,
the velocity, denoted ![]() , is a vector with three components for
the x, y and z motion.
, is a vector with three components for
the x, y and z motion.
To see this a little more clearly, look at the path of the car along the road shown below. At each point on the road, the velocity points in the direction of the car's longitudinal axis. This means that the velocity vector of the car remains tangent to the path of the car's motion.
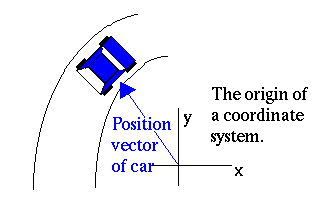
What do we know of that is related to tangents? You guessed it, derivatives. One way to think of this is to look at the change in the car's position over time. Form a difference quotient and take the limit as the distance between points on the car's path shrinks to zero. This will produce the result that
| (2) |
The speed of the car is the magnitude of the velocity. Thus
| (3) |