Distance Along a Curve

If a particle travels at speed s in a straight line for an interval of time $\Delta t$ how far does it travel total? The total distance (as we all know from distance equals rate times time) is $s \Delta t$. What if s = s(t), that is s is not constant? Then we simply integrate over the time interval $\Delta t = b - a$ to get $\int_a^b s(t) dt$. In more general motion in three dimensions, the speed is the magnitude of the velocity, so the total distance traveled along a path $\vec{r}(t)= x(t)\hat{i} + y(t)\hat{j} + z(t)\hat{k}$ as t varies from a to b is

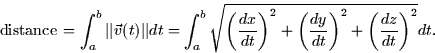$$\mbox{distance} \thinspace = \int_a^b \vert\vert \vec{v}(t) ... ...( \frac{dy}{dt} \right)^2 + \left( \frac{dz}{dt} \right)^2} dt.$$ (5)

Be careful, though, the next example illustrates what can happen if the velocity becomes equal to $\vec{0}$ at some point. As it turns out, in this case, you only get the total displacement over time interval, not the total distance traveled.

Example. A particle moves along the path

$$\vec{r}(t) = \cos \frac{\pi}{2}(1-t)^2 \hat{i} + \sin frac{\pi}{2}(1-t)^2 \hat{j}.$$ (6)

How far does the particle travel from t = 0 to t = 2. Looking at the graph of the path of the particle, it is obvious that the particle travels a quarter of a circular arc of radius 1 twice: once in one direction and once in the opposite direction. So the total distance traveled by the particle should be $2 (1/4) (2 \pi) = \pi$. Let's see what the integral above tells us. Differentiating, we get

$$\vec{v}(t) = \pi (1 - t) [\sin \frac{\pi}{2}(1-t)^2 \hat{i} - \cos \frac{\pi}{2}(1-t)^2 \hat{j}], \mbox{and}$$ (7)

$$\vert\vert\vec{v}(t)\vert\vert = \pi (1-t)[\sin^2 \frac{\pi}{2}(1-t)^2 + \cos^2 \frac{\pi}{2}(1-t)^2] = \pi (1-t).$$ (8)

Thus, the total distance traveled, by the formula above is

$$\int_0^2 \vert\vert\vec{v}(t)\vert\vert dt = \pi \int_0^2 (1-t)dt = \pi \left[ t - \frac{1}{2}t^2\right]_0^2 = 0.$$ (9)

What happened? Notice that the velocity of the particle is $\vec{0}$ at t = 1. The particle then begins to retrace its path, but in the other direction, introducing a negative sign. Thus, the integral above really only gives the net displacement of the particle, not the distance traveled. To get the distance, we need to break the integral up into two pieces.

$$\mbox{distance} \thinspace = \left\vert\int_0^1 \vert\vert\v... ...ert\int_1^2 \vert\vert\vec{v}(t)\vert\vert dt\right\vert = \pi.$$ (10)