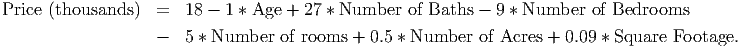
So far we have used only a single explanatory variable to describe the variation in our response variables. However, in real world data, there are usually complicated relationships involving many different variables. Consider the price of a home, for example. It depends on the size of the home, the condition of the home, the location of the home, the number of bedrooms, the number of bathrooms, the presence any amenities, and many other ”less tangible” qualities. If you were to use any single one of these to predict the price of the home, the model would have a very low coefficient of determination and a very high Se because the other variables are being ignored. In essence, a single-variable model for data like this tries to make all of the ”left out” variables the same. If we choose the size (in square feet) to predict price, we are basically saying that all houses that have the same number of square feet must also have the same number of bedrooms, the same number of bathrooms, the same location, the same condition, and the same amenities. Clearly this is not the case. This means that the variation in price caused by these ”left out” variables will result in a lot of spread around the regression line.
This problem is actually related to another issue with complex data. If you want to graph the data, each variable in the problem requires a separate dimension. One explanatory variable and one response variable requires two dimensions to graph (a plane). Two explanatory variables and one response require three dimensions to graph (space). Anything more requires more dimensions that we can represent on paper or with a physical, hands-on model. Thus, as we try to build models that incorporate more variables, we lose one of our main tools, scatterplots, for picturing the data. Without a scatterplot of the actual data (Y vs. all the X variables) we cannot use software to make a trendline. The only way to get the model equation is to use multiple regression.
Multiple regression produces longer, more complicated looking equations as models of the data. However, they are not more difficult to interpret than simple regression models. Suppose we use data on houses to produce a regression model that looks like
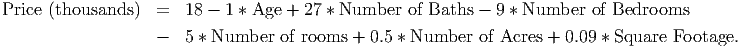
This model shows how each variable influences the price of the home when all of the other variables are controlled for. That is, by holding all the other explanatory variables constant. Notice, however, that since each variable has different units, the coefficients do not tell us which variables are most important. Each full bathroom in the home adds $27,000 to the sale price, but each square foot only adds $90. This does not mean that bathrooms are more important than size, though. In fact, an additional 300 square feet (a 15’ by 20’ room) adds exactly $27,000 to the price. Without looking at the units on each coefficient, you cannot say which are more important. In this section, you will learn how to build and interpret multiple regression models like this one.