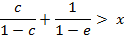Below, we will discuss criteria for having a high selectivity to the cross-product AB as opposed to the selectivity to symmetrical products AA and BB of a bimolecular reaction, A + B. The symmetry can be broken by polarizing roles of two components of the bimolecular reaction in opposite directions. If one reagent is a better electrophile, the other one must be a better nucleophile for the cross-selectivity to exceed the statistical binomial distribution.
Problem statement. In the cross-condensation of two acids A and B there are four products formed, BeAc, AeBc, AeAc, and BeBc by combinatorial paring of the enolic and carbonyl components (indicated by sub-indexes e and c). What are the products distribution based on the reactivity of the enolic and carbonyl components and the molar ratio of A to B? Specifically, we are interested in the condition of having the highest selectivity to the cross-condensation versus self-condensation of acids A and B.
Solution. We built a kinetic model based on the bimolecular reaction rate equations with dimensionless concentrations and length for making BeAc, AeBc, AeAc, and BeBc ketones.
(16a)
(16b)
(16c)
(16d)
The system of
differential equations (16) with the boundary
conditions, 
and
, for acid fractions B and A changing
with the conversion, was solved numerically to
obtain the product concentrations, 
depending
on coefficients 
, 
, 
, and 
. The integral
selectivities, 
, were obtained by normalization:
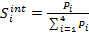(17)
We have
mathematically proven, that the sum of the
distribution functions 
and 
, which represent the
cross-ketone, deviate positively from the sum of
binomial probability functions 
, i.e. 
in two
cases, if
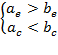(18a)
or if
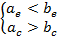(18b)
Under all other conditions, a negative deviation
was found, i.e. 
.
The significance. According
to the stated criterion, the highest
cross-selectivity will be observed when acids
A and B are separated in their roles, i.e. one
is preferentially serving as the enolic
component, while the other is the preferred
carbonyl component. In our experimental work
we have identified catalysts which can
discriminate two acids in their roles in the
reaction mechanism.
The mathematical proof is provided below.
Statement. Distribution
functions 
and 
, which represent the
cross-ketone, deviate positively from the
binomial probability functions 
and 
in two
cases, if
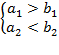(A.1a)
or if
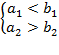(A.1b)
Analysis and proof by algebra methods.
The probability functions for making AeAc, AeBc, BeAc, and BeBc ketones respectively, on the basis of the binomial statistical approach are
(A.2a)
(A.2b)
(A.2c)
(A.2d)
where 
and 
, respectively.
Coefficients, 
, 
, 
, and 
, are assigned to
transform functions 
into 
.
(A.3a)
(A.3b)
(A.3c)
(A.3d)
Coefficients 
and 
represent acids A and B,
respectively. Subindexes 1 and 2 represent
the enolic and the carbonyl components,
respectively. Coefficients e 
, and 
have
the meaning of the relative activity of acid B vs.
acid A as
the enolic or as the carbonyl component,
respectively.
The adjusted
distribution functions 
are
obtained through normalization
and represent the differential selectivities to
the four products.
(A.4)
The denominator in eq. (A.4) can be transformed into a shorter form:
=
= 
(A.5)
After dividing
the numerator and the denominator by 
each function
is transformed into a new form:
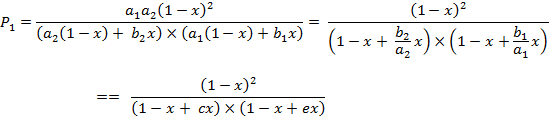
(A.6a)
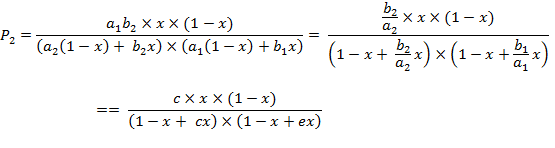
(A.6b)
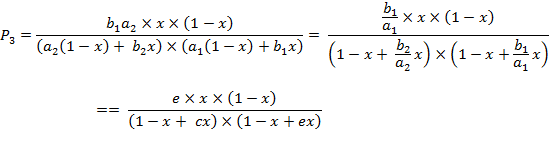
(A.6c)
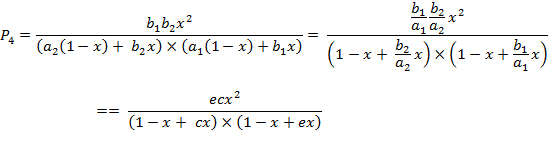
(A.6d)
The relation
between functions and is
analyzed separately under four different terms.
Results are summarized in Table A.1.
Table A.1. The
relation between and functions
under four terms.
|
Terms |
AA |
BB |
AB |
|
|
1) |
|
|
|
|
|
2) |
|
|
|
|
|
3) |
|
if
true
for any |
If
If |
If
|
|
4) |
|
|||
Function 
, term
1) 
, or 
. In this case
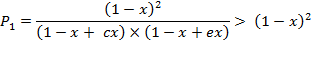
is true,
because if 
then 
. Similarly, 
, therefore the
denominator is less than 1, but the whole
fraction is greater than 1.
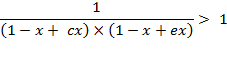
i.e. 
under
term 1.
Function , term
2) 
, or 
. Under
this term, it can be proven than
simply
by changing the sign in all equations obtained
under term 1) above, i.e., because , therefore, 
, and 
, therefore the
denominator is greater than 1, but the whole
fraction is less than 1.
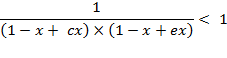
Therefore, under term 2.
Function , term
3) 
, or 
; and term
4) 
, or 
.
After
the next transformation, the criteria for a
negative deviation of 
from
the binomial value is:
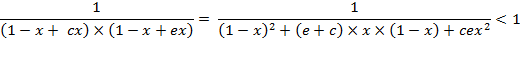
Or, it can be further transformed into the next form with the change of the inequality sign:
Because 
, the next form can be
obtained:
,
or, 
Further transformations provide the simplified criteria:
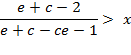
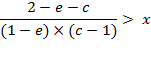
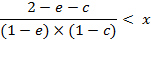
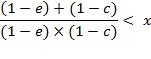
in the final form:
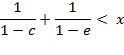
(A.7)
where 
.
For a positive
deviation of from
the binomial value the sign of the inequality
(A.7) is reversed:
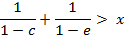
(A.8)
Under the terms
3 and 4, function can
deviate from the binomial value in both a
positive and negative way depending on 
and
parameters 
and 
. Condition for a region
of a negative deviation, independent of , is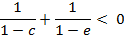 
Criteria for a
positive deviation, 
independent
of x can be found
from the condition:
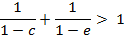
Which can be transformed into
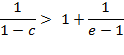
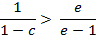
Function 
, term
1) , or .
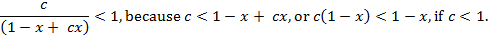
Similarly,
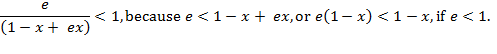
If each
multiplier is less than one, then the product is
also less than one, i.e. 
Function , term
2) , or . Changing
the sign in all equations under term 1 proves
that 
under
term 2.
Function , term
3) , or ; and term
4) , or .
A quick
solution for the negative deviation of 
from the binomial value
can be obtained by switching acids A and B in
equation A.7. Parameters and are
replaced by their reciprocal values, and is
replaced with 
.
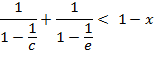
The last
equation can be modified to:
To find when
the negative deviation does not depend on , it is set to 
and
equation (A.9b) is transformed into 
, or
(A.10)
Equation (A.10)
is the criteria for having a negative deviation
of 
, i.e. 
For a positive
deviation, 
, regardless of , equation (A.9b) is
solved for 
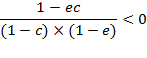
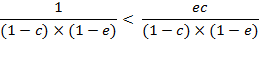
Functions 
, general
remarks for a positive deviation. To
preserve the unity of 
a
negative deviation of 
automatically
means a positive deviation of 
Condition for
having positive deviation of functions 
from
the binomial value can be obtained by combining
equations A.3b,
A.3c, A.6b, and A.6c
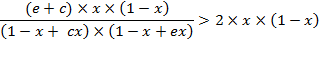
which gives
after transformation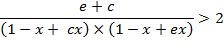
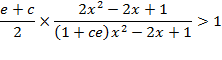
(A.11)
A sufficient,
but not necessary condition for the solution of
eq. (A.11) is given when each multiplicand is
greater than one: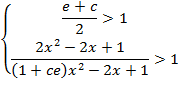 
or 
or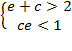 
(A.12)
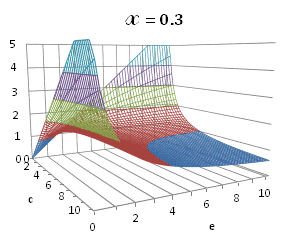
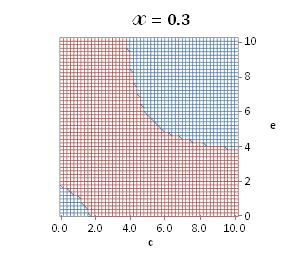
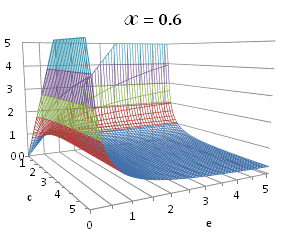
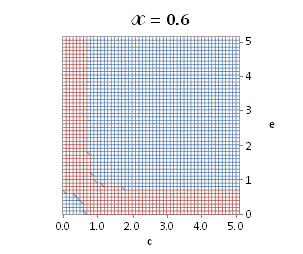
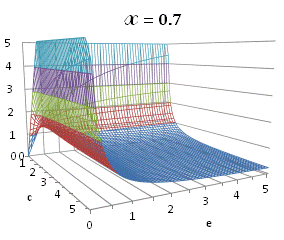
A more broad
solution for eq. (A.11) depending on is
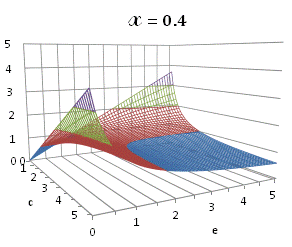
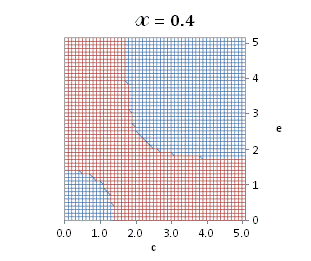
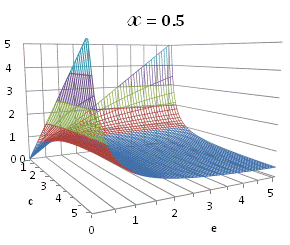
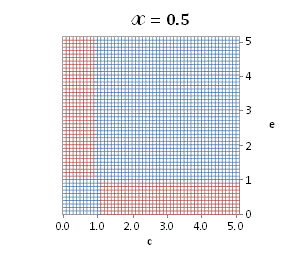
graphically illustrated in Fig. A.1.
a) 
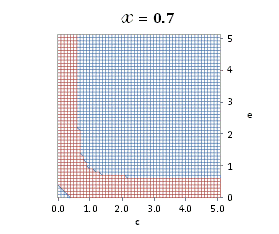b)
Fig. A.1. Graphical
illustration for the positive deviation of the
cross-selectivity, 
from
binomial functions 
for 
, represented by values
above 1.0 in eq. (A.11) as a) a
multi-colored 3D-graph (other than blue), and b) a
projection in (e,c)
coordinates (red colored area).
Functions , term
1) , or . Because , the first condition in
(A.12), 
is not true.
Functions , term
2) , or . Because , the second condition in
(A.12), 
is not satisfied.
Functions , terms
3) and 4). Under these
terms eq. (A.11) can be satisfied by eq. (A.12),
which is sufficient, but not necessary.
The behavior
of functions 
under
terms 1-4 is illustrated
by graphs in Figures A.2-A.5. Parameters and for
graphs in Figures A.2 and A.3 are chosen so as
to demonstrate the symmetry of graphs with
respect to the choice of acid, A and B,
i.e., 
and 
. Parameters under term 3
are those found for TK catalyst (Fig. A.4). An
example of parameters e and c in Fig. A.5
demonstrates the case when cross-selectivity can
change from positive to negative deviation
depending on the composition of acids’ mixture.
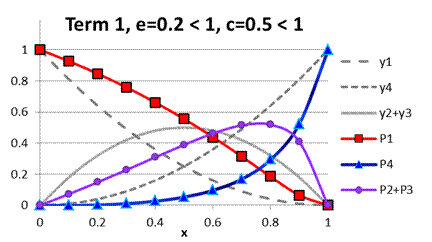
Fig. A.2. Comparison
of functions to under term 1, e
< 1, c < 1
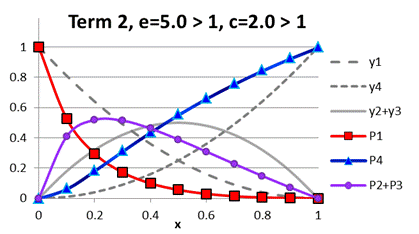
Fig. A.3. Comparison
of functions to under term 2, e
> 1, c > 1
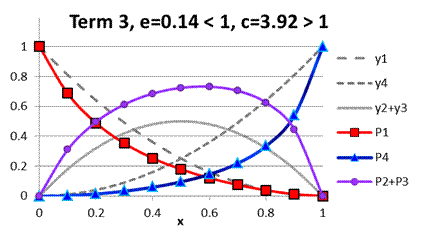
Fig. A.4. Comparison
of functions to under term 3,
e=0.14 < 1, c=3.92 > 1
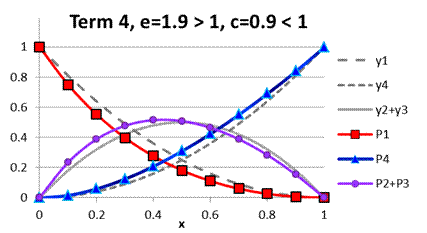
Fig. A.5. Comparison
of functions to under term 4, e=1.9
> 1, c=0.9 < 1
Everything
discussed above applies for the differential
selectivities. In order to get the integral
selectivities, a law for the reactants
concentration change along the length of the
flow reactor has to be known. However, for any
specific ratio of the two acids changing along
the reactor length, the specified criteria
(Table A.1) are still valid for calculating the
differential selectivities. Reactor model for TK
catalyst (Fig. A.6) shows selectivity graphs for
all products closely matching those
theoretically calculated for the same parameters 
and (Fig.
A.4).
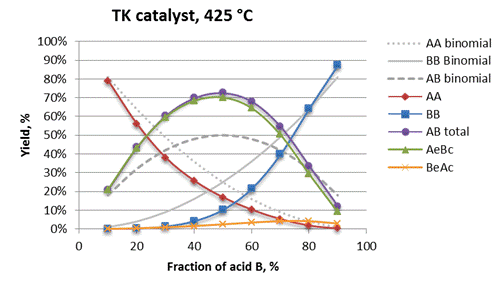
Fig. A.6. Integral
selectivities for the reactor model with TK
catalyst at temperature of 425 °C.
Conclusion. In
summary,
it has been shown that when
, then , but . On the other hand, if
, then 
, but 
If both conditions
are
satisfied, then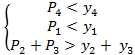 
.
This allows 
and 
to
exceed binomial functions 
.
The combined condition, 
requires
either 
, or 
For references,
please, cite this work as:
Ignatchenko,
A.V.; Deraddo, J.S.; Marino, V.J.; Mercado, A.
Cross-Selectivity in the catalytic
ketonization of carboxylic acids. Applied Catal. A: General, 498, 10-24, 2015.