Replacement of hexagons by heptagons in the graphene
honeycomb pattern creates a negative Gaussian
curvature leading to the deviation (Fig. 1) from the
graphene planar arrangement and induces ring closures.
The ring closure can be done symmetrically in several
ways which leads to different triply periodic minimal
surfaces (TPMS). We have recently discovered new
examples of the Gyroid, Schwartz P- and D-surfaces by
the {3,7} pattern, known as the
hyperbolic soccer ball. Click on
each image to explore 3D interactive model.

Fig. 1. A
beginning of the hyperbolic surface growth
by adding layers of heptagons around the
central one (shown in red). There are 7
heptagons in the first layer (grey), and
21 in the second layer (blue).
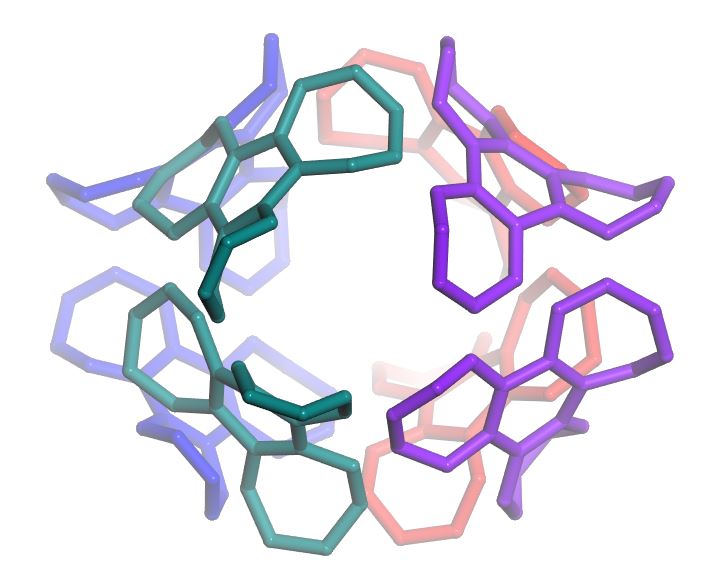
Fig. 3.
Schwartz P-surface
P130-C672
made out of heptagons with
tetragonal symmetry
different from the cubic symmetry
of P207-C168
because of a different
connectivity between
four pairs of adjacent
trimers.

